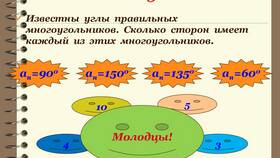
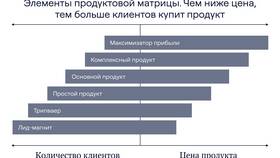
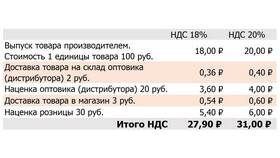
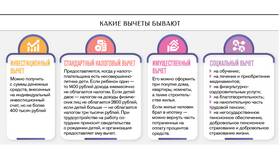
Сумма кубов двух чисел - это результат сложения кубов этих чисел. Математически это выражается формулой: a³ + b³, где a и b - любые действительные числа.
Содержание
Формула суммы кубов
Для вычисления суммы кубов двух чисел применяется следующая формула:
a³ + b³ = (a + b)(a² - ab + b²)
Примеры вычислений
| Числа | Вычисление | Результат |
| 1 и 2 | 1³ + 2³ = 1 + 8 | 9 |
| 3 и 4 | 3³ + 4³ = 27 + 64 | 91 |
| 5 и -2 | 5³ + (-2)³ = 125 + (-8) | 117 |
Свойства суммы кубов
- Коммутативность: a³ + b³ = b³ + a³
- Неассоциативность: (a³ + b³) + c³ ≠ a³ + (b³ + c³)
- При a = -b сумма кубов равна нулю
Разложение на множители
Сумму кубов можно разложить на множители:
a³ + b³ = (a + b)(a² - ab + b²)
Пример разложения
| Выражение | Разложение |
| x³ + 8 | (x + 2)(x² - 2x + 4) |
| 27 + y³ | (3 + y)(9 - 3y + y²) |
Применение суммы кубов
- Решение алгебраических уравнений
- Упрощение сложных выражений
- Доказательство математических теорем
- Вычислительная математика
Заключение
Сумма кубов двух чисел является важным алгебраическим понятием, которое находит применение в различных разделах математики. Знание формулы суммы кубов и ее свойств позволяет эффективно решать широкий круг математических задач.